Câu hỏi
Cho tứ diện đều \(ABCD\) có độ dài các cạnh bằng \(a\). Tính khoảng cách từ điểm \(A\) đến mặt
phẳng \(\left( {BCD} \right)\).
- A \(a\sqrt 6 \)
- B \(\dfrac{{a\sqrt 3 }}{2}\)
- C \(a\)
- D \(\dfrac{{a\sqrt 6 }}{3}\)
Lời giải chi tiết:
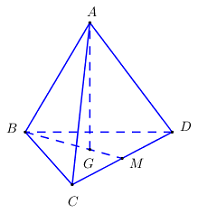
+ \(ABCD\) là tứ diện đều\( \Rightarrow \) Khoảng cách từ \(A\) đến \(\left( {BCD} \right)\) là đoạn \(AG\) với \(G\) là trọng tâm tam giác \(ABC\).
\( \Rightarrow BG = \dfrac{2}{3}BM = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\).
+ Xét tam giác \(ABG\) vuông tại \(G\) có :
\(A{G^2} = A{B^2} - B{G^2} = {a^2} - {\left( {\dfrac{{a\sqrt 3 }}{3}} \right)^2} = \dfrac{{2{a^2}}}{3} \Rightarrow AG = \dfrac{{a\sqrt 6 }}{3}\).
Chọn D
Câu hỏi trước
