Câu hỏi
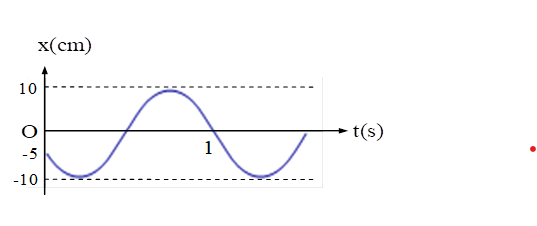
Một chất điểm dao động điều hòa có đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ như hình vẽ. Phương trình dao động của vật là:
- A \(x = 10\cos \left( {\frac{{11\pi }}{6}t + \frac{{2\pi }}{3}} \right)cm\)
- B \(x = 10\cos \left( {\frac{{11\pi }}{6}t - \frac{{2\pi }}{3}} \right)cm\)
- C \(x = 10\cos \left( {2\pi t + \frac{\pi }{3}} \right)cm\)
- D \(x = 10\cos \left( {\frac{{5\pi }}{6}t - \frac{\pi }{3}} \right)cm\)
Phương pháp giải:
Xác định A; ω và φ của phương trình: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Sử dụng VTLG xác định pha ban đầu.
Lời giải chi tiết:
Theo đồ thị ta thấy:
Biên độ dao động: A = 10cm
Thời gian chất điểm có li độ \(x=-\frac{A}{2}=-5cm\) đến lúc x = 0 và đi theo chiều âm là:
\(t=\frac{T}{2}+\frac{T}{4}+\frac{T}{6}=\frac{11T}{12}=1\text{s}\Rightarrow T=\frac{12}{11}s\Rightarrow \omega =\frac{11\pi }{6}\left( rad \right)\)
Gốc thời gian tại vị trí \(x = - \frac{A}{2} = - 5cm\) và đang giảm nên pha ban đầu: \(\varphi = \frac{{2\pi }}{3}\)
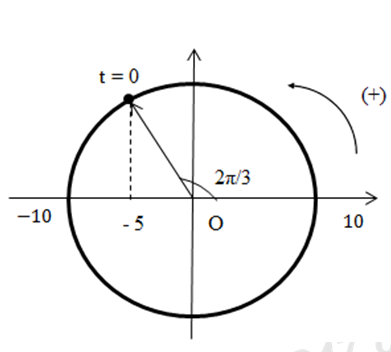
Phương trình dao động của vật là: \(x = 10\cos \left( {\frac{{11\pi }}{6}t + \frac{{2\pi }}{3}} \right)cm\)
Chọn A







