Phương pháp giải:

Xác định A; ω và φ của phương trình: \(x = A\cos \left( {\omega t + \varphi } \right)\)

Chu kì là khoảng thời gian vật thực hiện hết 1 dao động toàn phần \(T = \frac{{2\pi }}{\omega } = \frac{{\Delta t}}{N}\)

(Với N là số dao động thực hiện trong thời gian ∆t)

Công thức vận tốc cực đại: \({v_{\max }} = \omega A \Rightarrow A = \frac{{{v_{\max }}}}{\omega }\)

Sử dụng VTLG xác định pha ban đầu.

Lời giải chi tiết:

Chu kì dao động: \(T=\frac{20}{50}=0,4(s)\Rightarrow \omega =\frac{2\pi }{T}=5\pi (rad/s)\)

Vận tốc cực đại: \({{v}_{\max }}=\omega A\Rightarrow A=\frac{{{v}_{\max }}}{\omega }=\frac{20\pi }{5\pi }=4(cm)\)

Tại t = 0, vật đi qua VTCB theo chiều âm. Biểu diễn trên VTLG ta có: 

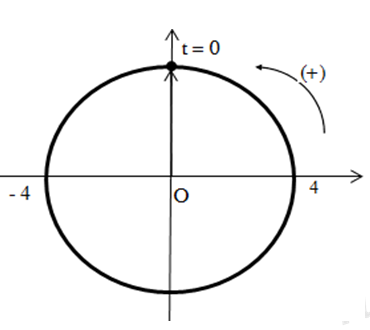
Từ VTLG xác định được  pha ban đầu \(\varphi =\frac{\pi }{2}\text{ }rad\)

→ PT dao động: \(x=4\cos \left( 5\pi t+\frac{\pi }{2} \right)cm\)

Chọn D