Phương pháp giải:

Xác định A; ω và φ của phương trình: \(x = A\cos \left( {\omega t + \varphi } \right)\)

Sử dụng VTLG xác định pha ban đầu.

Phương trình của vận tốc: \(v =  - \omega A\sin \left( {\omega t + \varphi } \right) = \omega A\cos \left( {\omega t + \varphi  + \frac{\pi }{2}} \right)\)

Lời giải chi tiết:

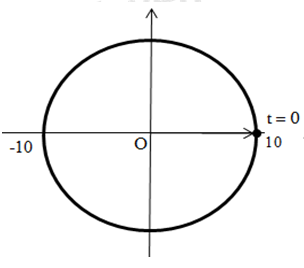
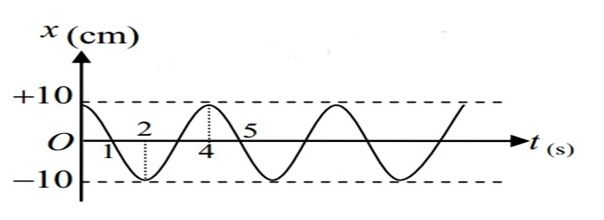
Từ đồ thị ta thấy:

+ Biên độ dao động A = 10 cm

+ Chu kì dao động: \(T = 4s \Rightarrow \omega  = \frac{{2\pi }}{T} = \frac{\pi }{2}{\rm{ }}rad/s\)

+ Tại t = 0, vật đang ở vị trí x = 10 cm → Pha ban đầu φ = 0 (rad) 

Phương trình của li độ: \(x=10.\cos \left( \frac{\pi }{2}t \right)\text{ }cm\Rightarrow v=-5\pi .\sin \left( \frac{\pi }{2}t \right)\text{ }cm/s\)

Chọn D