Lời giải chi tiết:

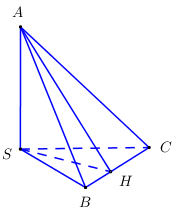
* \({V_{S.ABC}} = \dfrac{1}{3}.h.{S_{ABC}}\,\,\,\left( 1 \right)\).

* Ta có: \(h = d\left( {S;\left( {ABC} \right)} \right)\) (Khoảng cách từ \(S\) đến \(\left( {ABC} \right)\) chính là chiều cao kẻ từ đỉnh \(S\) xuống \(\left( {ABC} \right)\).

* \({V_{S.ABC}} = \dfrac{1}{3}.SA.{S_{ABC}} = \dfrac{1}{3}.1.\dfrac{1}{2}.2.3 = 1\).

* \({S_{ABC}} = \dfrac{1}{2}AH.BC\)

\(\left\{ \begin{array}{l}B{C^2} = \sqrt {S{B^2} + S{C^2}}  = \sqrt {4 + 9}  = \sqrt {13} \\\dfrac{1}{{S{H^2}}} = \dfrac{1}{{S{B^2}}} + \dfrac{1}{{S{C^2}}} = \dfrac{1}{4} + \dfrac{1}{9} = \dfrac{{13}}{{36}} \Rightarrow SH = \dfrac{6}{{\sqrt {13} }}\end{array} \right.\)

Xét tam giác vuông \(SAH:\,\,AH = \sqrt {S{A^2} + S{H^2}}  = \sqrt {1 + \dfrac{{36}}{{13}}}  = \dfrac{{7\sqrt {13} }}{{13}}\).

Vậy \({S_{ABC}} = \dfrac{1}{2}.\dfrac{{7\sqrt {13} }}{{13}}.\sqrt {13}  = \dfrac{7}{2} \Rightarrow 1 = \dfrac{1}{3}.\dfrac{7}{2}.h \Leftrightarrow h = \dfrac{6}{7}\).

Chọn C