Câu hỏi
Cho khối chóp \(S.ABC\) có \(SA\) vuông góc với đáy, \(SA = 4,\,\,AB = 6,\,\,BC = 10,\,\,CA = 8\). Tính thể tích
của khối chóp\(S.ABC\).
- A \(V = 40\)
- B \(V = 192\)
- C \(V = 32\)
- D \(V = 24\)
Lời giải chi tiết:
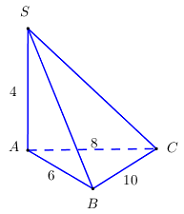
+ Xét tam giác \(ABC\) có \(AB = 6,\,\,AC = 8,\,\,BC = 10\).
Thấy \(\left\{ \begin{array}{l}A{B^2} + A{C^2} = {6^2} + {8^2} = 100\\B{C^2} = {10^2} = 100\end{array} \right. \Rightarrow \Delta ABC\) vuông tại \(A\) (Pytago đảo).
\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.6.8 = 24\,\,\left( {dvdt} \right)\).
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.4.24 = 32\,\,\left( {dvtt} \right)\).
Chọn C
Câu hỏi trước
