Câu hỏi
Cho tứ diện \(ABCD\) có \(AB,\,\,AC,\,\,AD\) đôi một vuông góc với nhau, \(AB = a,\,\,AC = b,\,\,AD = c.\) Tính thể tích V của khối tứ diện ABCD theo \(a,\,b,\,c\)
- A \(V = \dfrac{{abc}}{2}\)
- B \(V = \dfrac{{abc}}{6}\)
- C \(V = \dfrac{{abc}}{3}\)
- D \(V = abc\)
Lời giải chi tiết:
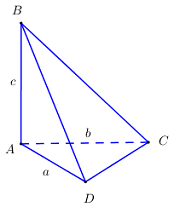
\({V_{S.ABC}} = \dfrac{1}{3}AB.{S_{ACD}} = \dfrac{1}{3}AB.\dfrac{1}{2}AC.AD = \dfrac{1}{6}abc\).
Chọn B
Câu hỏi trước
