Câu hỏi
Cho hình chóp \(S.ABCD\)có đáy \(ABCD\) là hình thoi cạnh \(a\), góc \(\widehat {ABC}\) bằng 600, cạnh bên \(SA\) vuông góc với đáy, \(SC\) tạo với đáy góc 600. Thể tích khối chóp \(S.ABCD\)là:
- A \(\dfrac{{{a^3}}}{2}\)
- B \(\dfrac{{{a^3}}}{3}\)
- C \(\dfrac{{{a^3}}}{{15}}\)
- D \(\dfrac{{{a^3}\sqrt 2 }}{2}\)
Lời giải chi tiết:
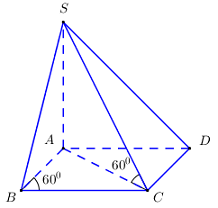
+ Xét tam giác \(ABC\) có \(\left\{ \begin{array}{l}AB = BC = a\\\widehat {ABC} = {60^0}\end{array} \right. \Rightarrow \Delta ABC\) đều \( \Rightarrow AC = a\).
+ Xét tam giác \(SAC\) vuông tại \(A:\,\,SA = AC.\tan {60^0} = a\sqrt 3 \).
+ \({S_{ABCD}} = 2{S_{ABC}} = 2.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^2}\sqrt 3 }}{2}\).
+ \({V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}.a\sqrt 3 .\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}}}{2}\).
Chọn A
Câu hỏi trước
