Lời giải chi tiết:

Ta có \(y = \sqrt {2x - {x^2}}  + 2019 \Rightarrow y' = {\left( {2x - {x^2}} \right)^{\dfrac{1}{2}}} + 2019\).

\( \Rightarrow y' = \dfrac{1}{2}{\left( {2x - {x^2}} \right)^{ - \dfrac{1}{2}}}\left( {2 - 2x} \right) \Leftrightarrow y' = \dfrac{{2 - 2x}}{{2\sqrt {2x - {x^2}} }} = \dfrac{{1 - x}}{{\sqrt {2x - {x^2}} }}\).

ĐK: \(0 < x < 2\). \(y' = 0 \Leftrightarrow x = 1\).

BBT:

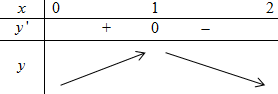
Vậy \({y_{\max }} = y\left( 1 \right) = 2020\).

Chọn B