Câu hỏi
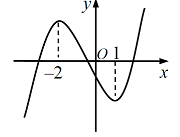
Cho đường cong \(\left( C \right):y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình bên. Khẳng định nào sau đây là đúng?
- A \(a > 0,b < 0,c < 0,d < 0\).
- B \(a > 0,b > 0,c < 0,d > 0\).
- C \(a < 0,b > 0,c > 0,d < 0\).
- D \(a > 0,b > 0,c < 0,d < 0\).
Lời giải chi tiết:
· Nét cuối đi lên \( \Rightarrow a > 0\).
· Với \(x = 0,\,\,y = d < 0\).
· Ta thấy \({x_1} = - 2;\,\,{x_2} = 1\) là 2 điểm cực trị của hàm số.
\(y' = 3a{x^2} + 2bx + c = 0\).
\({x_1} + {x_2} = - 1 < 0 \Rightarrow \dfrac{{ - 2b}}{{3a}} < 0\). Mà \(a > 0 \Rightarrow b > 0\).
\({x_1}{x_2} = - 2 < 0 \Leftrightarrow \dfrac{c}{{3a}} < 0\). Mà \(a > 0 \Rightarrow c < 0\).
Chọn D
Câu hỏi trước
