Lời giải chi tiết:

Gọi \(A\left( {m;3} \right)\) là những điểm thuộc \(y = 3\)

Phương trình đường thẳng qua \(A(m;3)\) có dạng: \(y = k\left( {x - m} \right) + 3.\)

Đường thẳng qua A và tiếp xúc với đồ thị \( \Rightarrow \left\{ \begin{array}{l} - 4{x^3} + 3x + 2 = k\left( {x - m} \right) + 3\\ - 12{{\rm{x}}^2} + 3 = k\end{array} \right.\)

\(\begin{array}{l} \Leftrightarrow 3 + \left( { - 12{x^2} + 3} \right)\left( {x - m} \right) =  - 4{x^3} + 3x + 2 \Leftrightarrow 8{x^3} - 12{x^2}.m + 3m - 1 = 0\\ \Leftrightarrow m\left( {3 - 12{x^2}} \right) = 1 - 8{x^3} \Leftrightarrow m = \dfrac{{1 - 8{x^3}}}{{3 - 12{x^2}}}\,\,\,\left( * \right)\end{array}\)

Để kẻ được 3 đường thẳng tiếp xúc với đồ thị \( \Rightarrow \) Phương trình (*) phải có 3 nghiệm.

Xét \(f\left( x \right) = \dfrac{{1 - 8{x^3}}}{{3 - 12{x^2}}}\,\,\,\left( {DK:\,\,\,x \ne  \pm \dfrac{1}{2}} \right)\)

\(\begin{array}{l}f'\left( x \right) = \dfrac{{ - 24{x^2}\left( {3 - 12{x^2}} \right) + \left( {1 - 8{x^3}} \right)24x}}{{{{\left( {3 - 12{x^2}} \right)}^2}}} = 0\\ \Leftrightarrow 24x\left[ {\left( {1 - 8{x^3}} \right) - x\left( {3 - 12{x^2}} \right)} \right] = 0\\ \Leftrightarrow 24x\left( {1 - 8{x^3} - 3x + 12{x^3}} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\,\,\,\,\left( {tm} \right)\\x =  - 1\,\,\,\left( {tm} \right)\\x = \dfrac{1}{2}\,\,\,\,\,\left( {loai} \right)\end{array} \right.\end{array}\)

Bảng biến thiên:

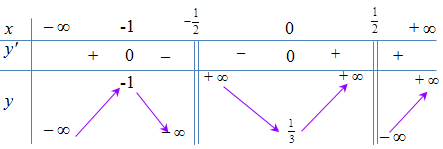
PT (*) có 3 nghiệm \( \Rightarrow \) Đường thẳng \(y = m\) phải cắt đồ thị tại 3 điểm \( \Leftrightarrow \left[ \begin{array}{l}m < - 1\\m > \dfrac{1}{3}\end{array} \right..\)

Chọn B