Lời giải chi tiết:

+ Lập phương trình đường thẳng đi qua\(M(1;2)\)

\( \Rightarrow \)Phương trình đường thẳng có dạng:\(y = k\left( {x - {x_0}} \right) + {y_0}\)

                                         \( \Leftrightarrow y = k\left( {x - 1} \right) + 2 \Leftrightarrow y = kx - k + 2\)

Đường thẳng qua M và tiếp xúc với Đồ thị

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}{x^3} - 2{x^2} + (m - 1)x + 2m = kx - k + 2\\3{x^2} - 4x + (m - 1) = k\end{array} \right.\\ \Leftrightarrow {x^3} - 2{x^2} + mx - x + 2m = 3{x^3} - 4{x^2} + mx - x - 3{x^2} + 4x - m + 1 + 2\\ \Leftrightarrow 2{x^3} - 5{x^2} + 4x + 3 = 3m\,\,(*)\end{array}\)

Để kẻ được 2 tiếp tuyến đến đồ thị \( \Rightarrow \) PT (*) phải có 2 nghiệm

Xét \(f\left( x \right) = 2{x^3} - 5{x^2} + 4x + 3\)

\(f'\left( x \right) = 6{x^2} - 10x + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \dfrac{2}{3}\end{array} \right.\)

BBT:

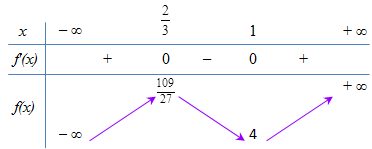
PT (*) có 2 nghiệm \( \Rightarrow \) Đường thẳng\(y = 3m\) phải cắt đồ thị tại 2 điểm \( \Leftrightarrow \left[ \begin{array}{l}3m = \dfrac{{109}}{{27}}\\3m = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{{109}}{{81}}\\m = \dfrac{4}{3}\end{array} \right..\)

Chọn A