Phương pháp giải:

+ Gọi điểm trên trục tung là \(M\left( {0;m} \right)\)

+ Lập phương trình đường thẳng đi qua\(M\left( {0;m} \right)\)

\( \Rightarrow \) Phương trình đường thẳng có dạng:\(y = k\left( {x - {x_0}} \right) + {y_0} \Leftrightarrow y = k.\left( {x - 0} \right) + m \Leftrightarrow y = kx + m\)

Đường thẳng tiếp tuyến qua \(M\) và tiếp xúc với đồ thị \( \Rightarrow \left\{ \begin{array}{l}kx + m = {x^4} - {x^2} + 1\,\,\,\,\left( 1 \right)\\k = 4{x^3} - 2x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Thế (2) vào (1) ta được:

\(\begin{array}{l} \Leftrightarrow m =  - \left( {4{x^3} - 2x} \right)x + {x^4} - {x^2} + 1\\ \Leftrightarrow m =  - 4{x^4} + 2{x^2} + {x^4} - {x^2} + 1\\ \Leftrightarrow m =  - 3{x^4} + {x^2} + 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left(  *  \right)\end{array}\)

+ Để kẻ được 3 tiếp tuyến tới đồ thị thì PT (*) phải có 3 nghiệm.

Xét \(f\left( x \right) =  - 3{x_{}}^4 + {x_{}}^2 + 1\)

\(f'\left( x \right) =  - 12{x_{}}^3 + 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{\sqrt 6 }}{6}\\x =  - \dfrac{{\sqrt 6 }}{6}\\x = 0\end{array} \right.\)

BBT:

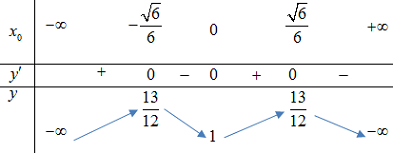
Để PT (*) có 3 nghiệm  \( \Rightarrow \) Đường thẳng\(y = m\) phải cắt đồ thị tại 3 điểm \( \Leftrightarrow m = 1.\)

Vậy điểm cần tìm là \(M\left( {0;1} \right).\)

Chọn A