Lời giải chi tiết:

\(y = \frac{{x - 1}}{{x + 3}} \Rightarrow y' = \frac{4}{{{{\left( {x + 3} \right)}^2}}}\)

Phương trình tiếp tuyến tại M có dạng: \(y = y'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\)

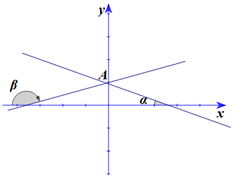
Do \(OB = 4OA \Rightarrow \left[ \begin{array}{l}{\rm{hsg tt}} = \tan \alpha  = \frac{1}{4}\\{\rm{hsg tt}} = \tan \beta  = \frac{{ - 1}}{4}\end{array} \right.\)

\(\begin{array}{l} \Rightarrow \left[ \begin{array}{l}\frac{4}{{{{\left( {{x_0} + 3} \right)}^2}}} = \frac{1}{4}\\\frac{4}{{{{\left( {{x_0} + 3} \right)}^2}}} = \frac{{ - 1}}{4}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{\left( {{x_0} + 3} \right)^2} = 16\\{\left( {{x_0} + 3} \right)^2} =  - 16\,\,\,\left( {loai} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{x_0} + 3 = 4\\{x_0} + 3 =  - 4\end{array} \right. \Rightarrow \left[ \begin{array}{l}{x_0} = 1\\{x_0} =  - 7\end{array} \right. \Rightarrow \left[ \begin{array}{l}{y_0} = 0\\{y_0} = 2\end{array} \right.\end{array}\)

Vậy \(M\left( {1;0} \right)\) và \(M\left( { - 7;2} \right)\).

Chọn A.