Lời giải chi tiết:

Xét phương trình hoành độ giao điểm: \({x^3} - 3{x^2} - m = 0 \Leftrightarrow {x^3} - 3{x^2} = m\).

Đặt \(f\left( x \right) = {x^3} - 3{x^2}\)

Khảo sát và vẽ bảng biến thiên của \(f\left( x \right)\) bằng MODE 7:

B1: Nhập \(f\left( x \right) = {x^3} - 3{x^2}\).

B2:      Start: \( - 5\)

           End: \(5\)

           Step: \(10/19\).

Ta thu được đồ thị  của \(f\left( x \right)\) như sau:

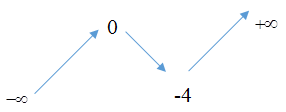
\( \Rightarrow \)Đường thẳng \(y = m\) cắt \(f\left( x \right)\) tại 3 điểm phân biệt \( \Leftrightarrow m \in \left( { - 4;0} \right)\).

Chọn D