Câu hỏi
Cho hàm số \(y = f\left( x \right)\)xác định trên \(\mathbb{R}\backslash \left\{ 0 \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
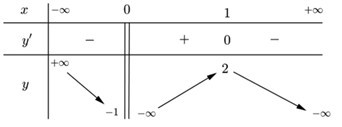
Tìm tập hợp tất cả các giá trị của tham số m sao cho phương trình \(f\left( x \right) = m\) có đúng hai nghiệm thực?
- A \(\left( { - \infty ; - 1} \right) \cup \left\{ 2 \right\}\)
- B \(\left( { - \infty ;2} \right)\)
- C \(\left( { - \infty ;2} \right]\)
- D \(\left( { - \infty ;-1} \right] \cup \left\{ 2 \right\}\)
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm: \(\left( { - \infty ; - 1} \right) \cup \left\{ 2 \right\}\)
Bảng biến thiên:
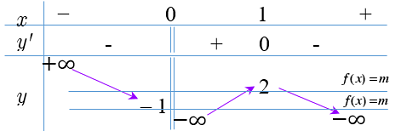
Để phương trình \(f\left( x \right) = m\) có đúng 2 nghiệm thì đường thẳng \(y = m\) phải nằm ở 2 vị trí như trên hìn \( \Rightarrow \left[ \begin{array}{l}m = 2\\m < - 1\end{array} \right..\)
+ Xét \(m = - 1\), tại vị trí \( - 1\) cho ra nghiệm\(x = 0\)(Không xác định)
\( \Rightarrow \) Tại \( - 1\) chỉ cắt 2 điểm \( \Rightarrow \)\(m = - 1\) vẫn thỏa mãn \( \Rightarrow \left[ \begin{array}{l}m = 2\\m \le - 1\end{array} \right..\)
Chọn D







