Câu hỏi
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\backslash \left\{ 0 \right\}\) và có bảng biến thiên như hình dưới.
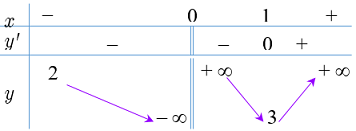
Hỏi phương trình \(3\left| {f(x)} \right| - 10 = 0\) có bao nhiêu nghiệm?
- A 2 nghiệm.
- B 4 nghiệm.
- C 3 nghiệm.
- D 1 nghiệm.
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm: \(3\left| {f\left( x \right)} \right| - 10 = 0 \Leftrightarrow \left| {f\left( x \right)} \right| = \dfrac{{10}}{3} \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = \dfrac{{10}}{3}\\f\left( x \right) = - \dfrac{{10}}{3}\end{array} \right.\)
Bảng biến thiên:
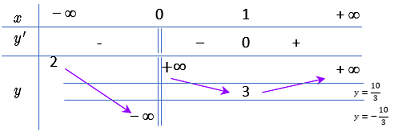
+ Dựa vào BBT trên ta thấy đường thẳng \(y = \dfrac{{10}}{3} \approx 3,3\) cắt đồ thị \(y = f\left( x \right)\) (là các mũi tên màu tím) tại 2 điểm phân biệt (Chú ý 3,3 nằm trên 2 nên ko thể cắt tại chỗ dưới số 2 kia được).
+ Dựa vào BBT trên ta thấy đường thẳng \(y = \dfrac{{ - 10}}{3} \approx - 3,3\) cắt đồ thị \(y = f\left( x \right)\)(là các mũi tên màu tím) tại 1 điểm phân biệt.
\( \Rightarrow \)Tổng số nghiệm của phương trình là 3.
Chọn C







