Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đồ thị dưới đây. Tìm tất cả các giá trị của m để phương trình \(f\left( {\left| x \right|} \right) = m\) có 3 nghiệm phân biệt :
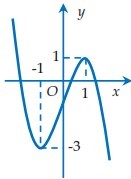
- A \( - 1 < m < 1\)
- B \(m = - 3\)
- C \( - 3 < m < 1\)
- D \(m = - 1\)
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm:\(f\left( {\left| x \right|} \right) = m.\)
+ Để phương trình có 3 nghiệm phân biệt thì đường thẳng \(y = m\)phải cắt đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\)tại 3 điểm phân biệt
+ Nhận thấy đồ thị đề bài cho là đồ thị hàm số \(y = f\left( x \right)\), nên ta vẽ lại đồ thị \(y = f\left( {\left| x \right|} \right)\)như hình dưới bằng cách:
B1: Lấy đối xứng nét đồ thị bên phải trục Oy sang bên trái
B2: Xóa bỏ các nét đồ thị bên trái trục Oy
B3: Các nét đồ thị còn lại là đồ thị cần tìm
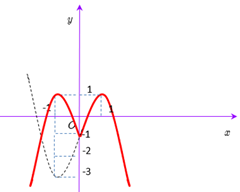
Dựa vào hình vẽ. Để cắt tại 3 điểm phân biệt thì\(y = m\) phải nằm tại \( - 1\)\( \Leftrightarrow m = - 1.\)
Chọn D







