Câu hỏi
Hình vẽ bên là đồ thị của hàm số \(y = {x^3} - 3x - 1\). Giá trị của m để phương trình \(\left| {{x^3} - 3x - 1} \right| = m\) có 3 nghiệm đôi một khác nhau là:
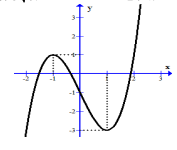
- A \(1 < m < 3\)
- B \(m = 0\)
- C \(m = 0,m = 3\)
- D \( - 3 < m < 1\)
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm: \(\left| {{x^3} - 3x - 1} \right| = m\,\)
+ Để phương trình trên có 3 nghiệm \( \Rightarrow \)Đồ thị hàm số \(y = \left| {{x^3} - 3x - 1} \right|\)phải cắt đường thẳng \(y = m\)tại 3 điểm phân biệt.
+ Nhận thấy đồ thị ở đề bài là đồ thị của hàm số \(y = {x^3} - 3x - 1\). Nên ta vẽ lại đồ thị hàm số \(y = \left| {{x^3} - 3x - 1} \right|\) như hình bên dưới bằng cách:
B1: Lấy đối xứng những nét đồ thị phía dưới trục Ox lên trên
B2: Gạch bỏ những nét đồ thị phía dưới trục Ox (nét đồ thị âm)
B3: Các nét đồ thị còn lại là đồ thị cần tìm
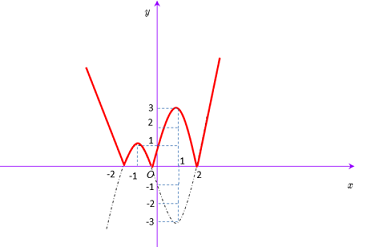
Dựa vào đồ thị. Để cắt tại 3 điểm đôi một khác nhau thì \(y = m\)phải nằm tại 0 và 3 \( \Rightarrow \left[ \begin{array}{l}m = 3\\m = 0\end{array} \right..\)
Chọn C







