Câu hỏi
Đồ thị trong hình bên dưới là đồ thị của hàm số \(y = - {x^4} + 4{x^2}\). Dựa vào đồ thị bên dưới hãy tìm tất cả các giá trị thực của tham số m sao cho phương trình \({x^4} - 4{x^2} + m - 2 = 0\) có hai nghiệm?
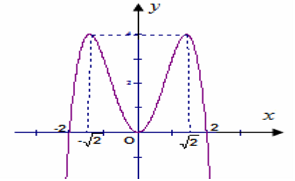
- A \(m < 2\)
- B \(m < 0,m = 4\)
- C \(m < 2,m = 6\)
- D \(m < 0\)
Lời giải chi tiết:
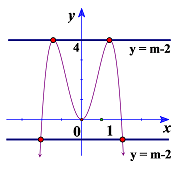
Phương trình:\({x^4} - 4{x^2} + m - 2 = 0 \Leftrightarrow m - 2 = - {x^4} + 4{x^2}\)
+ Để phương trình có 2 nghiệm \( \Rightarrow \)Đường thẳng \(y = m - 2\)phải cắt đồ thị hàm số \(y = - {x^4} + 4{x^2}\)tại 2 điểm phân biệt
+ Dựa vào đồ thị ta thấy \(y = m - 2\)phải nằm tại 4 và nằm dưới 0
\( \Rightarrow \left[ \begin{array}{l}m - 2 = 4\\m - 2 < 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 6\\m < 2\end{array} \right..\)
Chọn C
Câu hỏi trước
