Lời giải chi tiết:

+ TCĐ:

Mẫu = 0 \( \Rightarrow x - m + 2 = 0 \Leftrightarrow x = m - 2\).

Tử = 0: \(x =  - m\).

Để có TCĐ thì nghiệm mẫu \( \ne \)nghiệm tử \( \Rightarrow m - 2 \ne  - m \Leftrightarrow m \ne 1\)

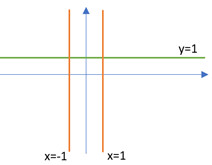
+ TCN: \(y = 1\).

Để TCĐ và TCN của đồ thị hàm số cùng 2 trục toạ độ tạo thành hình chữ nhật có \(S = 1\) thì

Tiệm cận đứng phải là 2 vị trí màu cam như hình

\( \Rightarrow \left\{ \begin{array}{l}x = m - 2 = 1\\x = m - 2 =  - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 3\,\,\,\left( {tm} \right)\\m = 1\,\,\left( {loai} \right)\end{array} \right.\)

Chọn D.