 Môn Toán - Lớp 12
Môn Toán - Lớp 12
 40 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ vận dụng, vận dụng cao
40 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ vận dụng, vận dụng cao
Câu hỏi
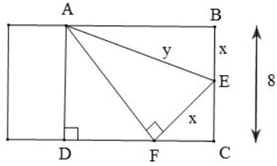
Cho một tờ giấy hình chữ nhật với chiều dài \(12{\rm{ }}cm\) và chiểu rộng\(8{\rm{ }}cm\). Gấp góc bên phải của tờ giấy sao cho sau khi gấp, đỉnh của góc đó chạm đáy dưới như hình vẽ. Để độ dài nếp gấp là nhỏ nhất thì giá trị nhỏ nhất đó bằng bao nhiêu?
- A \(6\sqrt 3 \).
- B \(6\sqrt 2 \).
- C \(6\sqrt 5 \).
- D \(6\).
Lời giải chi tiết:
\(CF = \sqrt {{x^2} - {{\left( {8 - x} \right)}^2}} = \sqrt {16x - 64} \)
đồng dạng với \(\Delta FCE \Rightarrow \dfrac{{EF}}{{AF}} = \dfrac{{CF}}{{AD}} \Rightarrow AF = \dfrac{{EF.AD}}{{CF}} = \dfrac{{8x}}{{\sqrt {16x - 64} }}\)
\(\begin{array}{l}AE = y = \sqrt {A{F^2} + E{F^2}} = \sqrt {\dfrac{{64{x^2}}}{{16x - 64}} + {x^2}} = \sqrt {\dfrac{{16{x^3}}}{{16x - 64}}} \\AE\,\min \Leftrightarrow {y^2}\min \\{y^2} = f\left( x \right) = \dfrac{{16{x^3}}}{{16x - 64}} \Rightarrow f'\left( x \right) = \dfrac{{48{x^2}\left( {16x - 64} \right) - 16.16{x^3}}}{{{{\left( {16x - 64} \right)}^2}}}\\ \Leftrightarrow x = 6\end{array}\)
BBT:
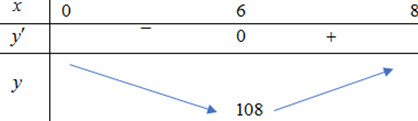
\({y_{\min }} = \sqrt {f{{\left( x \right)}_{\min }}} = \sqrt {108} = 6\sqrt 3 \)
Chọn A.






