Câu hỏi
Người ta cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng \(\dfrac{{500}}{3}{m^3}\). Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là \(500.000\) đồng/m2. Hãy xác định kích thước của hồ nước sao cho chi phí thuê nhân công thấp nhất và chi phí đó là:
- A \(74\) triệu đồng.
- B \(75\) triệu đồng
- C \(76\) triệu đồng.
- D \(77\) triệu đồng.
Lời giải chi tiết:
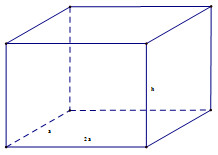
Goi chiều rộng đấy là \(a\)
\( \Rightarrow \)Chiều dài đấy là \(2a\)
Ta có \(V = \dfrac{{500}}{3} \Rightarrow a.2a.h = \dfrac{{500}}{3} \Rightarrow h = \dfrac{{500}}{{3.2{a^2}}}\)
\({S_{tp}} = a.2a + 2\left( {ah} \right) + 2\left( {2ah} \right) = 2{a^2} + 2a.\dfrac{{500}}{{6{a^2}}} + 4a.\dfrac{{500}}{{6{a^2}}}\)
\( \Rightarrow \)Chi phí thuê người xây hồ là:\(C = 500\left( {2{a^2} + 2a.\dfrac{{500}}{{6{a^2}}} + 4a.\dfrac{{500}}{{6{a^2}}}} \right)\)
\( \Rightarrow \)Tìm GTNN của \(C\):
MODE 7: \(f\left( x \right)\): Nhập hàm số \(\left. \begin{array}{l}Start:0\\End:10\\Step:\dfrac{{10}}{{19}}\end{array} \right\} \Rightarrow GTNN\,\,F\left( x \right) \approx 75000\)
Chọn B.







