Câu hỏi
Gọi \(n,\,\,d\) lần lượt là số tiệm cận ngang, tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{x - 1}}{{\sqrt {2{x^2} - 1} - 1}}\). Mệnh đề nào sau đây đúng?
- A \(n + d = 1\)
- B \(n + d = 2\)
- C \(n + d = 3\)
- D \(n + d = 4\)
Lời giải chi tiết:
\(y = \dfrac{{x - 1}}{{\sqrt {2{x^2} - 1} - 1}}\)
Bấm máy:
+ Nếu \(x \to + \infty \)
CALC \(X = 999999999999\)
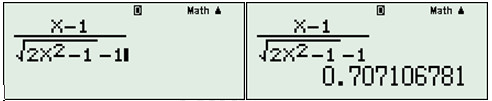
\(\Rightarrow \) TCN: \(y = 0,707.\)
+ Nếu \(x \to - \infty \)
CALC \(X = - 999999999999\)
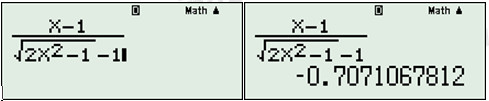
\( \Rightarrow \)TCN: \(y=-0,707\)
Có \(2\) TCN\( \Rightarrow n = 2.\)
* Tìm TCĐ: Cho Mẫu = 0
\( \Leftrightarrow \sqrt {2{x^2} - 1} = 1 \Leftrightarrow 2{x^2} - 1 = 1 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
+ Cho tử = 0 \( \Leftrightarrow x = 1\)
+ Điều kiện hàm số: \(2{x^2} - 1 \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 0,7\\x \ge 0,7\end{array} \right.\)
\( \Rightarrow \) \(x = - 1\) thỏa mãn \( \Rightarrow \)Có \(1\) TCĐ\( \Rightarrow d = 1.\)
Vậy \(n + d = 3.\)
Chọn C.
Câu hỏi trước
