Câu hỏi
Tìm GTLN , GTNN của hàm số lượng giác \(y = f(x) = 2\sin x + \cos 2x\) trên đoạn \(\left[ {0;\pi } \right]\)
- A \(\,Max\,f\left( x \right)=1;Min\,f\left( x \right)=\dfrac{2}{3}.\)
- B \(\,Max\,f\left( x \right)=1;Min\,f\left( x \right)=-\dfrac{3}{2}.\)
- C \(\,Max\,f\left( x \right)=\dfrac{3}{2};Min\,f\left( x \right)=-1.\)
- D \(\,Max\,f\left( x \right)=\dfrac{3}{2};Min\,f\left( x \right)=1.\)
Lời giải chi tiết:
\(y = f\left( x \right) = 2.\sin x + cos2x = \,2.\sin x + 1 - 2{\sin ^2}x\)
Đặt \(\sin \,x = t \Rightarrow t \in \left[ {0;1} \right].\)
Ta có: \(f\left( t \right) = 2t + 1 - 2{t^2}\)với \(t \in \left[ {0;1} \right]\)\( \Rightarrow f'\left( t \right) = 2 - 4t = \,0 \Leftrightarrow t = \dfrac{1}{2}\,\,\,\,\left( {tm} \right)\)
BBT:
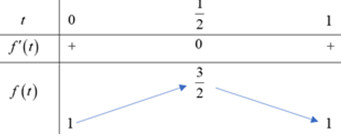
\(KL:\,Max\,f\left( x \right)=\dfrac{3}{2};Min\,f\left( x \right)=1.\)
Câu hỏi trước
