Lời giải chi tiết:

Cách 1: làm tay

\(y = f\left( x \right) = {\sin ^3}x - cos2x + \sin x + 2\)

\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,{\sin ^3}x - \left( {1 - 2{{\sin }^2}x} \right) + \sin x + 2\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,{\sin ^3}x + 2{\sin ^2}x + \sin x + 1.\end{array}\)

Đặt \(\sin x = t\left( { - 1 \le t \le 1} \right)\) và \(t \in \left[ { - 1;1} \right]\)\( \Rightarrow f\left( t \right) = {t^3} + 2{t^2} + t + 1.\)

Bài toán chuyển về Tìm GTLN và GTNN của hàm số \(f\left( t \right) = {t^3} + 2{t^2} + t + 1\)trên đoạn\(\left[ { - 1;1} \right]\)

+ TXĐ: \(D = \left[ { - 1;1} \right]\)

+ \(f'\left( t \right) = 3{t^2} + 4t + 1\)

Cho \(f'\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t =  - \dfrac{1}{3}\,\,\left( {tm} \right)\\t =  - 1\,\,\,\,\left( {tm} \right)\end{array} \right.\)

Thay  \(t =  - \dfrac{1}{3} \Rightarrow f\left( {\dfrac{{ - 1}}{3}} \right) = \dfrac{{23}}{{27}} = 0,851\)

Thay \(t =  - 1\) \( \Rightarrow f\left( { - 1} \right) = 1\)

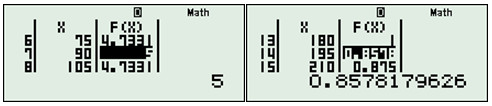
Thay \(t = 1\) \( \Rightarrow f\left( 1 \right) = 5\)

\(KL:\,Max\,f\left( x \right) = 5;\,Min\,f\left( x \right) = \dfrac{{23}}{{27}}.\)

Cách 2: Bấm máy

+ B1: Chuyển máy về Độ bấm: Shift + Mode + 3

+ B2: Tăng TABLE lên 40 dòng bấm: Shift + Mode  + \( \downarrow \)  + 5 + 1:\(f\left( x \right)\)

+ B3: Dùng máy tính cầm tay, chức năng TABLE (Mode + 7)

Nhập \(\left\{ \begin{array}{l}f(x) = {\sin ^3}x - \cos 2x + \sin x + 2\\Start:0\\End:360\\Step:15\end{array} \right.\)                   

Vậy \(GTLN = 5\) và \(GTNN = 0,8578\)