Câu hỏi
Tìm GTLN , GTNN của các hàm số sau: \(y = f(x) = - 3{x^2} + 4x - 8\) trên đoạn \([ - 4;3]\)
- A \( max f\left( x \right) = \,\dfrac{{ - 20}}{3},\,\,\min f\left( x \right) = \, - 72.\)
- B \( max f\left( x \right) = \,\dfrac{{ 20}}{3},\,\,\min f\left( x \right) = \, - 72.\)
- C \( max f\left( x \right) = \,\dfrac{{ - 20}}{3},\,\,\min f\left( x \right) = \, - 12.\)
- D \( max f\left( x \right) = \,\dfrac{{ 22}}{3},\,\,\min f\left( x \right) = \, - 72.\)
Lời giải chi tiết:
Cách 1: Tự luận
+ TXĐ: \(D = \left[ { - 4;3} \right]\).
+ \(y' = \,f'\left( x \right) = \, - 6x + \,4.\)
Cho \(y' = \,0\, \Leftrightarrow \, - 6x + \,4 = \,0 \Leftrightarrow x = \dfrac{2}{3}\,\,\left( {tm} \right)\)
\(\begin{array}{l}f\left( {\dfrac{2}{3}} \right) = \, - 3.\,{\left( {\dfrac{2}{3}} \right)^2} + 4\,.\dfrac{2}{3} - \,8 = \,\dfrac{{ - 20}}{3}.\\f\left( { - 4} \right) = \, - 3.{\left( { - 4} \right)^2} + \,4.\,\left( { - 4} \right) - \,8 = \, - 72.\\f\left( 3 \right) = \, - 3.\,{3^2} + \,4.\,3 - \,8 = \, - 23.\end{array}\)
\( \Rightarrow \,\max f\left( x \right) = \,\dfrac{{ - 20}}{3},\,\,\min f\left( x \right) = \, - 72.\)
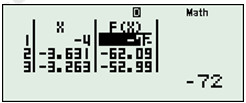
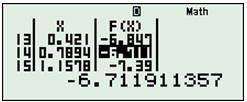
Cách 2: Bấm máy
Dùng máy tính cầm tay, chức năng TABLE (Mode + 7)
Nhập \(\left\{ \begin{array}{l}f(x) = - 3{x^2} + 4x - 8\\g(x):bo\,\,qua\\Start: - 4\\End:3\\Step\dfrac{7}{{19}}\end{array} \right.\)
Vậy \(GTLN = - 6,711\) và \(GTNN = - 72\).