Lời giải chi tiết:

+ B1: Đặt ẩn phụ \(\sin x = t\) \( \Rightarrow y = \dfrac{{ - 2t - 1}}{{t - m}}\)  

+ Đổi khoảng: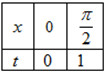 

\(\Rightarrow \) Đổi về bài toán tìm m để hàm số \(y=\dfrac{-2t-1}{t-m}\) đồng biến trên khoảng \(t\in \left( 0;1 \right)\).

+ B2: Làm như bình thường

Để hàm số đồng biến \(\Rightarrow y'>0\Leftrightarrow \dfrac{2m+1}{{{\left( t-m \right)}^{2}}}>0\Leftrightarrow m>\dfrac{-1}{2}\) 

+ Lại có ddiều kiện:  \(t\ne m\Leftrightarrow m\ne t\)  (Đặt trọng tâm vào m)

Mà \(t\in \left( 0;1 \right) \Rightarrow \) bắc cầu \(m \ne \left( {0;1} \right) \Leftrightarrow \left[ \begin{array}{l}m \le 0\\m \ge 1\end{array} \right.\).

Kết hợp lại ta có: \(\left[ \begin{array}{l}m \ge 1\\\dfrac{{ - 1}}{2} < m \le 0\end{array} \right.\).

Chọn C.