Lời giải chi tiết:

+ Đặt ẩn phụ \(\sin x=t\) \(\Rightarrow y=\dfrac{t+m}{t-1}\)

Đổi khoảng: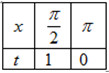 

\(\Rightarrow \) Đổi về bài toán tìm m để hàm số \(y = \dfrac{{t + m}}{{t - 1}}\) đồng biến trên khoảng \(t\in \left( 0;1 \right)\).

+ Vì hàm số đồng biến trên \(\left( 0;1 \right)\) \(\Rightarrow y'>0\Leftrightarrow \dfrac{-1-m}{{{\left( t-1 \right)}^{2}}}>0\Leftrightarrow m<-1\)

+ Lại có điều kiện: \(t \ne 1\) (Luôn đúng vì \(t \in \left( {0;1} \right)\))

Vậy \(m <  - 1.\)

Chọn B.