Câu hỏi
Tìm tập hợp các giá trị của tham số m để hàm số \(y = \sqrt {{x^2} + 1} - mx - 1\) đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\):
- A \(\left( { - \infty ; - 1} \right]\)
- B \(\left( { - \infty ; - 1} \right)\)
- C \(\left[ { - 1;1} \right]\)
- D \(\left[ {1; + \infty } \right)\)
Lời giải chi tiết:
\(y=\sqrt{{{x}^{2}}+1}-mx-1\Rightarrow y'=\dfrac{2x}{2\sqrt{{{x}^{2}}+1}}-m=\frac{x}{\sqrt{{{x}^{2}}+1}}-m\).
Để hàm số đồng biến trên \(( - \infty ; + \infty )\) \(\Leftrightarrow y'\ge 0\,\,\forall x\in \mathbb{R}\).
\(\Leftrightarrow \dfrac{x}{\sqrt{{{x}^{2}}+1}}-m\ge 0\Leftrightarrow m\le \dfrac{x}{\sqrt{{{x}^{2}}+1}}\Leftrightarrow m\le \underset{\left( -\infty ;+\infty \right)}{\mathop{\min }}\,\left( \dfrac{x}{\sqrt{{{x}^{2}}+1}} \right)\).
Dùng máy tính cầm tay, chức năng TABLE (Mode + 7)
Nhập \(\left\{ \begin{array}{l}f\left( x \right) = \dfrac{x}{{\sqrt {{x^2} + 1} }}\\g(x):bo\,\,qua\\Start: - 5\\End:5\\Step\dfrac{{10}}{{19}}\end{array} \right.\) \( \Rightarrow Min = - 0,98 = - 1\)\( \Rightarrow m \le - 1\).
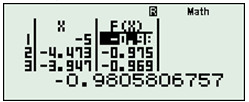
Chọn A.







