Lời giải chi tiết:

\(\begin{array}{l}y = {x^3} - 3\left( {m + 1} \right){x^2} + 3m\left( {m + 2} \right)x.\\ \Rightarrow y' = 3{x^2} - 6\left( {m + 1} \right)x + 3m\left( {m + 2} \right)\end{array}\)

Để hàm số nghịch biến trên đoạn \(\left[ {0;1} \right]\, \Leftrightarrow \,y' \le 0\,\)trên đoạn \(\left[ {0;1} \right]\)

\( \Leftrightarrow 3{x^2} - 6\left( {m + 1} \right)x + 3m\left( {m + 2} \right) \le 0\) (Không cô lập được \(m\)).

\(\Delta  = 36{\left( {m + 1} \right)^2} - 36m\left( {m + 2} \right) = 36\left( {{m^2} + 2m + 1} \right) - 36{m^2} - 72m. = 36.\)

\( \Rightarrow \left[ \begin{array}{l}{x_1} = \dfrac{{6\left( {m + 1} \right) + \sqrt {36} }}{6} = \dfrac{{6\left( {m + 1} \right) + 6}}{6} = m + 2\\{x_2} = \dfrac{{6\left( {m + 1} \right) - \sqrt {36} }}{6} = \dfrac{{6\left( {m + 1} \right) - 6}}{6} = m\end{array} \right.\)

BBT:

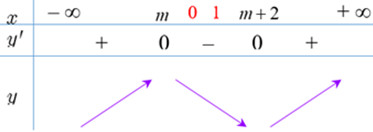
+ Đề hàm số nghịch biến trên \(\left[ {0;1} \right]\) thì số 0 và \(1\)  phải nằm giữa \(m\) và \(m + 2\) như BBT trên

\( \Rightarrow \left\{ \begin{array}{l}m + 2 \ge 1\\m \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ge  - 1\\m \le 0\end{array} \right. \Rightarrow  - 1 \le m \le 0.\)

Chọn A.