Lời giải chi tiết:

\(y = m{x^3} - {x^2} + 3x + m - 2 \Rightarrow y' = 3m{x^2} - 2x + 3\)

TH1: Xét\(m = 0\)

\( \Rightarrow y' =  - 2x + 3\)mà \(x \in \left( { - 3;0} \right) \Rightarrow y' > 0\forall x \in \left( { - 3;0} \right).\)

\( \Rightarrow \)Hàm số luôn đồng biến trên khoảng \(\left( { - 3;0} \right)\). Vậy \(m = 0\) thỏa mãn

TH2: Xét\(m \ne 0\, \Rightarrow y' = 3m{x^2} - 2x + 3 \ge 0\)

\( \Leftrightarrow 3m{x^2} \ge 2x - 3 \Leftrightarrow m \ge \dfrac{{2x - 3}}{{3{x^2}}} \Leftrightarrow m \ge \mathop {\max }\limits_{\left( { - 3;0} \right)} \left( {\,\dfrac{{2x - 3}}{{3{x^2}}}} \right)\)

Dùng máy tính cầm tay, chức năng TABLE (Mode + 7)

Nhập \(\left\{ \matrix{f\left( x \right) = {{2x - 3} \over {3{x^2}}} \hfill \cr g\left( x \right)\,:bo\,\,qua \hfill \cr Start: - 3 \hfill \cr End:0 \hfill \cr Step{3 \over {19}} \hfill \cr} \right.\) \( \Rightarrow Max = \dfrac{{ - 1}}{3}\)

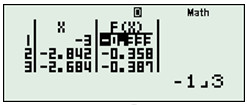
Mà theo đánh giá trên \(m \ge \max  \Rightarrow m \ge \dfrac{{ - 1}}{3}\).

Chọn D.