Câu hỏi
Trong khẳng định sau đây về hàm số \(y=\dfrac{{{x}^{2}}}{x-1}\), hãy tìm khẳng định đúng?
- A Hàm số có 1 điểm cực trị.
- B Hàm số có 1 cực đại và 1 cực tiểu.
- C Hàm số đồng biến trên từng trên từng khoảng xác định.
- D Hàm số nghịch biến trên từng trên từng khoảng xác định.
Lời giải chi tiết:
Ta có \(y' = \dfrac{{2x\left( {x - 1} \right) - {x^2}}}{{{{\left( {x - 1} \right)}^2}}} = \dfrac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}}\)
\( \Rightarrow y' = 0 \Rightarrow {x^2} - 2x = 0 \Rightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
Ta có bảng biến thiên:
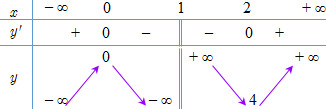
Như vậy hàm số có 1 cực đại và 1 cực tiểu.
Chọn B.
Câu hỏi trước
