Câu hỏi
Cho hàm số \(y=x-\sin 2x\). Mệnh đề nào dưới đây là đúng:
- A Hàm số đạt cực đại tại \(x=-\dfrac{\pi }{6}+k\pi \)
- B Hàm số đạt cực tiểu tại \(x=-\dfrac{\pi }{6}+k\pi \)
- C Hàm số không có điểm cực trị
- D Hàm số luôn luôn đồng biến trên R
Lời giải chi tiết:
Ta có \(y' = 1 - 2\cos 2x = 0 \Leftrightarrow \cos 2x = \dfrac{1}{2} = \cos \left( {\dfrac{\pi }{3}} \right)\)
\( \Rightarrow \left[ \begin{array}{l}2x = \dfrac{\pi }{3} + k2\pi \\2x = - \dfrac{\pi }{3} + k2\pi \end{array} \right. \Rightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k\pi \\x = - \dfrac{\pi }{6} + k\pi \end{array} \right.\)
Ta có bảng biến thiên:
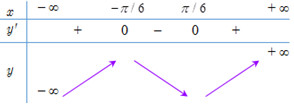
Dựa vào bảng biến thiên, hàm số đạt cực đại tại \(x=-\dfrac{\pi }{6}.\)
Chọn A.
Câu hỏi trước
