Câu hỏi
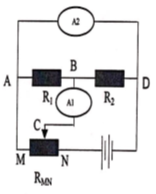
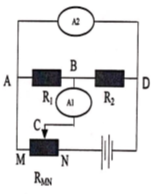
Mạch điện mắc như hình vẽ. Bộ nguồn gồm hai nguồn giống nhau, mỗi pin có suất điện động điện trở các Ampe kế và dây nối không đáng kể.
a) Nêu cấu tạo mạch ngoài khi con chạy C ở một vị trí giữa M và N.
b) Xác định vị trí của C để am pe kế A2 chỉ 0,3A?
Phương pháp giải:
a) Cấu tạo mạch ngoài:
\(\left[ {{R_{CN}}nt({R_{MC}}//{R_1}//{R_2})} \right]\)
b) Áp dụng định luật Ôm cho toàn mạch và cho đoạn mạch.
Lời giải chi tiết:
Tóm tắt:
2 nguồn giống nhau:
a) Nêu cấu tạo mạch ngoài khi con chạy C ở một vị trí giữa M và N.
b) Xác định vị trí của C để am pe kế A2 chỉ 0,3A?
Giải:
a) Cấu tạo mạch ngoài:
\(\left[ {{R_{CN}}nt({R_{MC}}//{R_1}//{R_2})} \right]\)
b) Gọi điện trở phần MC là x, phần CN = 6 -x
Ta có:
\({R_N} = {R_{CN}} + \frac{{{R_1}{R_2}{R_{MC}}}}{{{R_1}{R_2} + {R_1}{R_{MC}} + {R_2}{R_{MC}}}} = \frac{{12x - 2{x^2} + 18}}{{2x + 3}}\,\,\,\,(1)\)
Suất điện động và điện trở trong của bộ nguồn là:
\(\left\{ \begin{array}{l}
{E_b} = 2E = 2.1,5 = 3V\\
{r_b} = 2r = 2.0,5 = 1\Omega
\end{array} \right.\)
Ta lại có:
\(I = \frac{{{E_b}}}{{{R_N} + {r_b}}} \Leftrightarrow {E_b} = I({R_N} + {r_b})\,\,\,\,\left( 2 \right)\)
Hiệu điện thế mạch ngoài:
\({U_N} = {E_b} - I{r_b} = 3 - I\)
Ta có:
\({U_{NC}} = I(6 - x)\)
\({U_{BD}} = {U_N} - {U_{NC}} = (3 - I) - I(6 - x) = 3 - 7I + xI \Rightarrow {I_{BD}} = \frac{{{U_{BD}}}}{{{R_2}}} = \frac{{3 - 7I - xI}}{2}\,\,\,\left( 3 \right)\)
Từ giả thiết: \({I_{A2}} = 0,3A;\) tại nút D
\({I_{A2}} = I - {I_{BD}} \Leftrightarrow 0,3 = I - \frac{{3 - 7I + xI}}{2} \Rightarrow I = \frac{{18}}{{5(9 - x)}}\,\,\,\,\left( 4 \right)\)
Thay (4) vào (2) ta được:
\(3 = \frac{{18}}{{5(9 - x)}}\left( {\frac{{12x - 2{x^2} + 18}}{{2x + 3}} + 1} \right) \Leftrightarrow 2{x^2} - 9x + 9 = 0\)
Giải phương trình ta được
\(\left[ \begin{array}{l}
x = 3\Omega \\
x = 1,5\Omega
\end{array} \right.\)