Phương pháp giải:

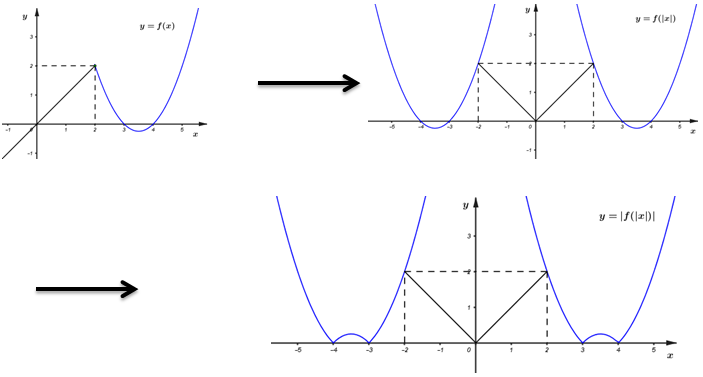
+) Vẽ đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) theo các bước sau:

B1: Giữ nguyên đồ thị \(y = f\left( x \right)\) ở bên phải \(Oy.\)

B2: “Xoá hẳn” đồ thị bên trái \(Oy.\)

B3: Lấy đối xứng qua \(Oy\) phần đồ thị bên phải \(Oy\) sang trái.

+) Vẽ đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\)theo các bước sau:

B1: Giữ nguyên đồ thị \(y = f\left( x \right)\) \(\left( C \right)\) ở phía trên trục \(Ox.\)

B2: Xoá phần đồ thị \(\left( C \right)\) ở phía dưới \(Ox.\)

B3: Lấy đối xứng phần đồ thị \(\left( C \right)\) phía dưới lên trên qua trục \(Ox.\)

+) Số nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) là số giao điểm của hai đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right).\)

Lời giải chi tiết:

Ta có đỉnh của parabol \(y = {x^2} - 7x + 12\) là  \(I\left( {\frac{7}{2};\,\, - \frac{1}{4}} \right).\)

Từ đồ thị hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\)ta thấy:

 Phương trình  \(\left| {f\left( {\left| x \right|} \right)} \right| = m\)có 6 nghiệm phân biệt \( \Leftrightarrow \frac{1}{4} < m < 2\)

Mà \(m \in \mathbb{Z} \Rightarrow m = 1\)

Chọn A.