Phương pháp giải:

Cho hàm số \(y = a{x^2} + bx + c{\rm{ }}\left( {a \ne 0} \right)\)

Với \(a > 0:\) Giá trị nhỏ nhất của hàm số \({y_{\min }} =  - \frac{\Delta }{{4a}}\) đạt được tại \(x =  - \frac{b}{{2a}}.\)

 Với \(a < 0:\) Giá trị lớn nhất của hàm số \({y_{\max }} =  - \frac{\Delta }{{4a}}\) đạt được tại \(x =  - \frac{b}{{2a}}.\)

Lời giải chi tiết:

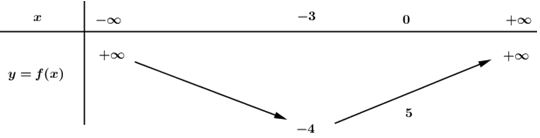
Ta có BBT của hàm số \(y = f\left( x \right) = {x^2} + 6x + 5\) như sau:

Đặt \(t = f\left( x \right) = {x^2} + 6x + 5.\) Khi \( - 3 \le x \le 0\) thì từ BBT, ta thấy \( - 4 \le t \le 5.\)

Do đó ta có: \(y = f\left( {f\left( x \right)} \right) = f\left( t \right) = {t^2} + 6t + 5{\rm{ }}\left( { - 4 \le t \le 5} \right)\)

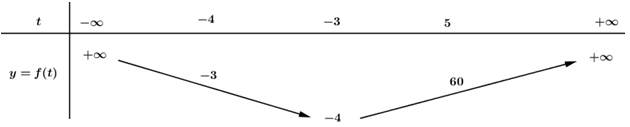
Ta có BBT của hàm \(f\left( t \right)\) trên như sau:

Từ BBT của hàm \(y = f\left( t \right)\) ta suy ra \(m = f\left( { - 4} \right) =  - 3;{\rm{ }}M = f\left( 5 \right) = 60\)

\( \Rightarrow S = m + M =  - 3 + 60 = 57.\)

Chọn C.