Phương pháp giải:

+) Vẽ đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) theo các bước sau:

B1: Giữ nguyên đồ thị \(y = f\left( x \right)\) ở bên phải \(Oy.\)

B2: “Xoá hẳn” đồ thị bên trái \(Oy.\)

B3: Lấy đối xứng qua \(Oy\) phần đồ thị bên phải \(Oy\) sang trái.

+) Vẽ đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\)theo các bước sau:

B1: Giữ nguyên đồ thị \(y = f\left( x \right)\) \(\left( C \right)\) ở phía trên trục \(Ox.\)

B2: Xoá phần đồ thị \(\left( C \right)\) ở phía dưới \(Ox.\)

B3: Lấy đối xứng phần đồ thị \(\left( C \right)\) phía dưới lên trên qua trục \(Ox.\)

+) Số nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) là số giao điểm của hai đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right).\)

Lời giải chi tiết:

Ta có phương trình  \(\left| {{x^2} - 4\left| x \right| - 5} \right| - m = 0 \Leftrightarrow \left| {{x^2} - 4\left| x \right| - 5} \right| = m\,\,\,\,\left( 1 \right).\)

Số nghiệm của phương trình \(\left( 1 \right)\) là số giao điểm của đồ thị hàm số \(y = \left| {{x^2} - 4\left| x \right| - 5} \right|\,\,\,\,\,\left( P \right)\) và đường thẳng \(y = m.\)

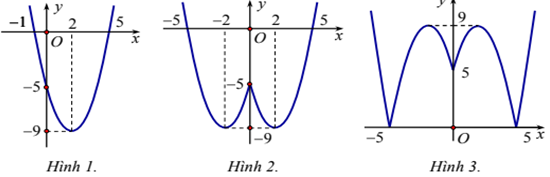
Xét hàm số \(y = {x^2} - 4x - 5\,\,\,\left( {{P_1}} \right)\) có đồ thị như hình 1:

Ta có hình 2 là đồ thị của hàm số \(y = {x^2} - 4\left| x \right| - 5\,\,\,\,\left( {{P_2}} \right)\) bằng cách:

+) Giữ nguyên đồ thị hàm số \(\left( {{P_1}} \right)\) phần bên phải \(Oy.\)

+) Lấy đối xứng phần 1 qua trục \(Oy.\)

Hình 3 chính là hình vẽ của đồ thị hàm số \(y = \left| {{x^2} - 4\left| x \right| - 5} \right|\,\,\,\,\left( P \right)\) bằng cách:

+) Giữ nguyên đồ thị hàm số \(\left( {{P_2}} \right)\) phần trên \(Ox\)

+) Lấy đối xứng đồ thị hàm số \(\left( {{P_2}} \right)\)phần dưới \(Ox\) qua trục \(Ox.\)

Quan sát đồ thị hàm số \((P)\) (hình 3), ta có:

\( \Rightarrow \left( 1 \right)\) có hai nghiệm phân biệt \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m > 9}\\{m = 0}\end{array}} \right.\) mà \(\left\{ {\begin{array}{*{20}{c}}{m \in \mathbb{Z}}\\{m \in \left( {0;2017} \right]}\end{array}} \right. \Rightarrow m \in \left\{ {10;11;12;...;2017} \right\}\)

Suy ra có: \(2017 - 10 + 1 = 2008\) số nguyên \(m\) thoả mãn bài toán.

Chọn  D.