Phương pháp giải:

Cho hàm số \(y = a{x^2} + bx + c{\rm{ }}\left( {a \ne 0} \right)\)

Với \(a > 0:\) Giá trị nhỏ nhất của hàm số \({y_{\min }} =  - \frac{\Delta }{{4a}}\) đạt được tại \(x =  - \frac{b}{{2a}}.\)

 Với \(a < 0:\) Giá trị lớn nhất của hàm số \({y_{\max }} =  - \frac{\Delta }{{4a}}\) đạt được tại \(x =  - \frac{b}{{2a}}.\)

Lời giải chi tiết:

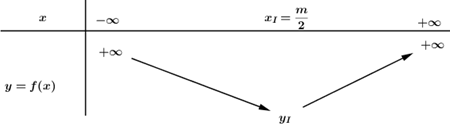
Parabol có hệ số theo \({x^2}\) là \(a = 4 > 0\) nên bề lõm hướng lên. Hoành độ đỉnh \({x_I} = \frac{m}{2}.\)

Ta có bảng biến thiên:

+) TH1:  \(\frac{m}{2} <  - 2 \Leftrightarrow m <  - 4 \Rightarrow {x_I} <  - 2 < 0 \Rightarrow \) Hàm số \(y = f\left( x \right)\) đồng biến trên đoạn \(\left[ { - 2;0} \right]\)

\( \Rightarrow \mathop {\min }\limits_{\left[ { - 2;0} \right]} f\left( x \right) = f\left( { - 2} \right) = {m^2} + 6m + 16.\)

Theo yêu cầu bài toán: \( \Rightarrow {m^2} + 6m + 16 = 3{\rm{ }} \Leftrightarrow {m^2} + 6m + 9 + 4 = 0 \Leftrightarrow {\left( {m + 3} \right)^2} + 4 = 0\) (vô nghiệm)

+) TH2:  \( - 2 \le \frac{m}{2} \le 0 \Leftrightarrow  - 4 \le m \le 0 \Rightarrow {x_I} \in \left[ { - 2;0} \right]\)

\( \Rightarrow y = f\left( x \right)\) đạt  GTNN  tại đỉnh \({x_I} = \frac{m}{2}.\)

\( \Rightarrow \mathop {\min }\limits_{\left[ { - 2;0} \right]} f\left( x \right) = f\left( {\frac{m}{2}} \right) =  - 2m\).

Theo yêu cầu bài toán: \( \Rightarrow  - 2m = 3 \Leftrightarrow m =  - \frac{3}{2}\,\,\,\left( {tm} \right)\)

+) TH3:  \(\frac{m}{2} > 0 \Leftrightarrow m > 0\) thì \({x_I} > 0 >  - 2 \Rightarrow \) Hàm số  \(y = f\left( x \right)\) nghịch biến trên \(\left[ { - 2;0} \right]\).

\( \Rightarrow \mathop {\min }\limits_{\left[ { - 2;0} \right]} f\left( x \right) = f\left( 0 \right) = {m^2} - 2m.\)

Theo yêu cầu bài toán: \( \Rightarrow {m^2} - 2m = 3 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m =  - 1\,\,\,\,\left( {ktm} \right)}\\{m = 3\,\,\,\,\,\left( {tm} \right)}\end{array}.} \right.\)

Vậy \(S = \left\{ { - \frac{3}{2};3} \right\} \Rightarrow T =  - \frac{3}{2} + 3 = \frac{3}{2}.\) 

Chọn  C.