Câu hỏi
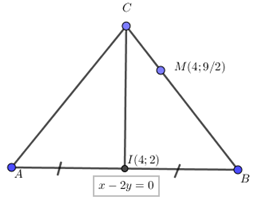
Trong mặt phẳng với hệ toạ độ \(Oxy,\) cho tam giác \(ABC\) cân tại \(C\) có diện tích bằng \(10,\) phương trình cạnh \(AB\) là \(x - 2y = 0\), điểm \(I\left( {4;2} \right)\) là trung điểm của \(AB\) và \(M\left( {4;\frac{9}{2}} \right)\) thuộc cạnh \(BC.\) Tìm toạ độ các đỉnh A, B, C biết tung độ điểm B lớn hơn hoặc bằng \(3.\)
- A \(A\left( {6;3} \right);B\left( {2;1} \right);C\left( {4;6} \right)\)
- B \(A\left( {2;1} \right);B\left( {6;3} \right);C\left( {2;6} \right)\)
- C \(A\left( {2;1} \right);B\left( {6;3} \right);C\left( { - 2;6} \right)\)
- D \(A\left( {2;1} \right);B\left( {6;3} \right);C\left( { - 2; - 6} \right)\)
Phương pháp giải:
\(\Delta ABC\) cân tại \(C \Rightarrow CA = CB.\)
Lời giải chi tiết:
Giả sử \(B\left( {2{y_B};{y_B}} \right) \in AB \Rightarrow A\left( {8 - 2{y_B};4 - {y_B}} \right).\)
Phương trình \(CI:\,\,2x + y - 10 = 0.\)
Gọi \(C\left( {{x_C};10 - 2{x_C}} \right) \Rightarrow \left| {\overrightarrow {CI} } \right| = \sqrt 5 \left| {4 - {x_C}} \right|;\left| {\overrightarrow {AB} } \right| = \sqrt {20} \left| {{y_B} - 2} \right|\)
\({S_{ABC}} = \frac{1}{2}CI.AB = 10 \Leftrightarrow \left| {4{y_B} + 2{x_C} - {x_C}{y_B} - 8} \right| = 2 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_C}{y_B} - 4{y_B} - 2{x_C} = - 6{\rm{ }}\left( 1 \right)}\\{{x_C}{y_B} - 4{y_B} - 2{x_C} = - 10{\rm{ }}\left( 2 \right)}\end{array}{\rm{ }}} \right.\)
Vì \(M \in BC \Rightarrow \overrightarrow {CM} = k\overrightarrow {MB} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{4 - {x_C} = k\left( {2{y_B} - 4} \right)}\\{ - \frac{{11}}{2} + 2{x_C} = k\left( {{y_B} - \frac{9}{2}} \right)}\end{array} \Rightarrow 2{x_C}{y_B} - 6{y_B} - 5{x_C} + 16 = 0{\rm{ }}\left( 3 \right)} \right.\)
Từ \(\left( 1 \right)\) và \(\left( 3 \right)\): \(\left\{ {\begin{array}{*{20}{c}}{{x_C}{y_B} - 4{y_B} - 2{x_C} = - 6}\\{2{x_C}{y_B} - 6{y_B} - 5{x_C} + 16 = 0}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{y_B} = - 1 - \sqrt 2 }\\{{y_B} = - 1 + \sqrt 2 }\end{array}\left( {loai \, \, do \,\, {{\rm{y}}_B} \ge 3} \right)} \right.} \right.\)
Từ \(\left( 2 \right)\) và \(\left( 3 \right)\):\(\left\{ {\begin{array}{*{20}{c}}{{x_C}{y_B} - 4{y_B} - 2{x_C} = - 10}\\{2{x_C}{y_B} - 6{y_B} - 5{x_C} + 16 = 0}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{y_B} = 3}\\{{x_C} = 2}\end{array}\left( {tm} \right)} \right.} \right.\)
Chọn C