Câu hỏi
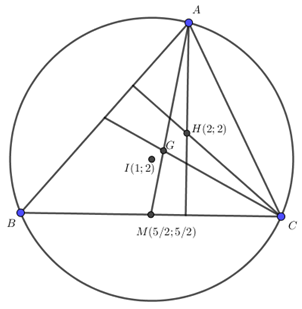
Trong mặt phẳng với hệ toạ độ \(Oxy,\) biết toạ độ trực tâm, tâm đường tròn ngoại tiếp tam giác \(ABC\) lần lượt là \(H\left( {2;2} \right);{\rm{ }}I\left( {1;2} \right)\) và trung điểm \(M\left( {\frac{5}{2};\frac{5}{2}} \right)\) của cạnh \(BC.\) Tìm toạ độ các đỉnh \(A,\, B,\, C\) biết \({x_B} > {x_C} \, ({x_B},{x_C}\) lần lượt là hoành độ của điểm \(B\) và \(C ).\)
- A \(A\left( { - 1;1} \right);B\left( { - 2;3} \right);C\left( {7;2} \right)\)
- B \(A\left( { - 1; - 1} \right);B\left( {3;1} \right);C\left( {2;4} \right)\)
- C \(A\left( {1; - 1} \right);B\left( {3;1} \right);C\left( {2;4} \right)\)
- D \(A\left( { - 1;1} \right);B\left( {3;1} \right);C\left( {2;4} \right)\)
Phương pháp giải:
Tâm của đường tròn ngoại tiếp tam giác là giao của ba đường trung trực trong tam giác.
Lời giải chi tiết:
Gọi \(G\) là trọng tâm \(\Delta ABC\) nên ta có \(\overrightarrow {GH} = - 2\overrightarrow {GI} \Rightarrow G\left( {\frac{4}{3};2} \right)\)
Mặt khác, vì \(\overrightarrow {GA} = - 2\overrightarrow {GM} \) nên \(A\left( { - 1;1} \right).\)
Phương trình \(BC:\,\,3x + y - 10 = 0.\)
Đường tròn \(\left( C \right)\) ngoại tiếp tam giác ABC có tâm \(I\left( {1;2} \right),\)bán kính \({\rm{R = }}\sqrt {4 + 1} = \sqrt 5 .\)
Do đó \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 5\)
Khi đó toạ độ \(B,\,\,C\) là nghiệm của hệ phương trình:\(\left\{ {\begin{array}{*{20}{c}}{{{\left( {x - 1} \right)}^2} + {{\left( {y - 2} \right)}^2} = 5}\\{3{\rm{x}} + y - 10 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{x = 2}\\{y = 4}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{x = 3}\\{y = 1}\end{array}} \right.}\end{array}} \right.} \right.\)
Vì \({x_B} > {x_C} \Rightarrow B\left( {3;1} \right),C\left( {2;4} \right)\)
Chọn D