Câu hỏi
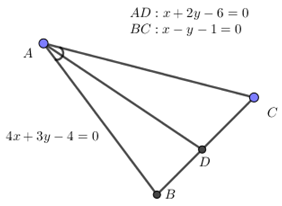
Trong mặt phẳng với hệ toạ độ \(Oxy,\) cho tam giác \(ABC\) biết phương trình các đường thẳng chứa cạnh \(AB,\, BC\) lần lượt là \(4x + 3y - 4 = 0;{\rm{ }}x - y - 1 = 0.\) Phân giác trong góc \(A\) nằm trên đường thẳng \(x + 2y - 6 = 0.\) Tìm toạ độ các đỉnh của tam giác \(ABC.\)
- A \(A\left( {2; - 4} \right);B\left( {1;0} \right);C\left( {5;4} \right)\)
- B \(A\left( { - 1;\frac{8}{3}} \right);B\left( {1;0} \right);C\left( {3;2} \right)\)
- C \(A\left( {4; - 4} \right);B\left( {1;0} \right);C\left( {5;4} \right)\)
- D \(A\left( {2; - 4} \right);B\left( {1;0} \right);C\left( {6;5} \right)\)
Phương pháp giải:
Sử dụng tính chất đường phân giác của tam giác để làm bài.
Lời giải chi tiết:
Toạ độ của A là nghiệm của hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{4x + 3y - 4 = 0}\\{x + 2y - 6 = 0}\end{array} \Rightarrow A\left( { - 2;4} \right)} \right.\)
Toạ độ của \(B\) là nghiệm của hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{4x + 3y - 4 = 0}\\{x - y - 1 = 0}\end{array} \Rightarrow B\left( {1;0} \right)} \right.\)
Phương trình \(AC\) qua điểm \(A\left( { - 2;4} \right)\) có dạng:\(a\left( {x + 2} \right) + b\left( {y - 4} \right) = 0 \Leftrightarrow ax + by + 2a - 4b = 0\)
Gọi \({\Delta _1}:4x + 3y - 4 = 0;{\rm{ }}{\Delta _2}:x + 2y - 6 = 0;{\rm{ }}{\Delta _3}:ax + by + 2a - 4b = 0\)
Từ giả thiết suy ra \(\angle \left( {{\Delta _2},{\Delta _3}} \right) = \angle \left( {{\Delta _1},{\Delta _2}} \right)\). Do đó:
\(\begin{array}{l}\cos \angle \left( {{\Delta _2},{\Delta _3}} \right) = \cos \angle \left( {{\Delta _1},{\Delta _2}} \right) \Leftrightarrow \frac{{\left| {1.a + 2.b} \right|}}{{\sqrt 5 .\sqrt {{a^2} + {b^2}} }} = \frac{{\left| {4.1 + 2.3} \right|}}{{\sqrt {25} .\sqrt 5 }}\\ \Leftrightarrow \left| {a + 2b} \right| = 2\sqrt {{a^2} + {b^2}} \Leftrightarrow a\left( {3{\rm{a}} - 4b} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{a = 0}\\{3a = 4b}\end{array}} \right.\end{array}\)
\(a = 0 \Rightarrow b \ne 0 \Rightarrow {\Delta _3}:y - 4 = 0\) \(3a - 4b = 0.\) chọn \(a = 4,b = 3 \Rightarrow {\Delta _3}:4x + 3y - 4 = 0\left( { \equiv {\Delta _1}} \right)\)Do vậy, phương trình của đường thẳng \(AC\) là \(y - 4 = 0\)
Toạ độ điểm \(C\) là nghiệm của hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{y - 4 = 0}\\{x - y - 1 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 5}\\{y = 4}\end{array} \Rightarrow C\left( {5;4} \right)} \right.} \right.\)
Chọn A