Câu hỏi
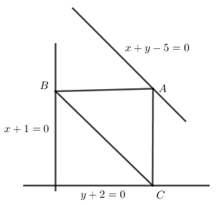
Trong mặt phẳng hệ toạ độ \(Oxy,\) cho tam giác \(ABC\) vuông cân tại \(A, \) biết các đỉnh \(A,\, B,\, C\) lần lượt nằm trên các đường thẳng \(\left( d \right):x + y - 5 = 0;{\rm{ }}\left( {{d_1}} \right):x + 1 = 0;{\rm{ }}\left( {{d_2}} \right):y + 2 = 0.\) Tìm toạ độ các đỉnh \(A,\, B,\, C\) biết \(BC = 5\sqrt 2 \) và tung độ của \(B\) không dương.
- A \(A\left( { - 3;8} \right);B\left( { - 1; - 3} \right);C\left( {6; - 2} \right)\)
- B \(A\left( {3;2} \right);B\left( { - 1; - 1} \right);C\left( {6; - 2} \right)\)
- C \(A\left( {3;2} \right);B\left( { - 1;3} \right);C\left( {4; - 2} \right)\)
- D \(A\left( {1;4} \right);B\left( { - 1; - 1} \right);C\left( {6; - 2} \right)\)
Phương pháp giải:
\(\Delta ABC\) vuông cân tại \(A \Rightarrow \left\{ \begin{array}{l}AB \bot AC\\AB = AC\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AB} .\overrightarrow {AC} = 0\\AB = AC\end{array} \right..\)
Lời giải chi tiết:
Chú ý: \({d_1} \bot {d_2}\) và \(\Delta ABC\) vuông cân tại \[A\] nên \[A\] cách đều \({d_1},{d_2}\)
Ta có: \(A \in d:\,\,\,x + y - 5 = 0 \Rightarrow A\left( {a;\,\,5 - a} \right).\)
\(\begin{array}{l} \Rightarrow d\left( {A;\,\,{d_1}} \right) = d\left( {A;\,\,{d_2}} \right) \Leftrightarrow \frac{{\left| {a + 1} \right|}}{1} = \frac{{\left| {5 - a + 2} \right|}}{1}\\ \Leftrightarrow \left| {a + 1} \right| = \left| {7 - a} \right|\\ \Leftrightarrow \left[ \begin{array}{l}a + 1 = 7 - a\\a + 1 = a - 7\end{array} \right. \Leftrightarrow a = 3 \Rightarrow A\left( {3;\,\,2} \right).\end{array}\)
Ta có: \(\left\{ \begin{array}{l}B \in {d_1} \Rightarrow B\left( { - 1;\,\,b} \right)\,\,\,\,\left( {b \le 0} \right)\\C \in {d_2} \Rightarrow C\left( {c; - 2} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AB} = \left( { - 4;\,\,b - 2} \right)\\\overrightarrow {AC} = \left( {c - 3;\,\, - 4} \right)\\\overrightarrow {BC} = \left( {c + 1;\,\, - 2 - b} \right)\end{array} \right..\)
\(\Delta ABC\) vuông cân tại \(A \Rightarrow AB \bot AC \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0.\)
Lại có \(BC = 5\sqrt 2 \Rightarrow B{C^2} = 50\)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l} - 4\left( {c - 3} \right) - 4\left( {b - 2} \right) = 0\\{\left( {c + 1} \right)^2} + {\left( {2 + b} \right)^2} = 50\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c - 3 = 2 - b\\{\left( {c + 1} \right)^2} + {\left( {2 + b} \right)^2} = 50\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}c = 5 - b\\{\left( {5 - b + 1} \right)^2} + {\left( {2 + b} \right)^2} = 50\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 5 - b\\2{b^2} - 8b - 10 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}c = 5 - b\\\left[ \begin{array}{l}b = 5\,\,\,\,\left( {ktm} \right)\\b = - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 1\\c = 6\end{array} \right. \Rightarrow \left\{ \begin{array}{l}B\left( { - 1; - 1} \right)\\C\left( {6; - 2} \right)\end{array} \right..\end{array}\)
Chọn B