Câu hỏi
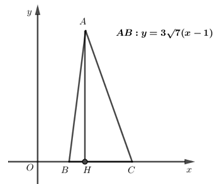
Trong mặt phẳng với hệ toạ độ \(Oxy,\) cho \(\Delta ABC\) cân có đáy \(BC.\) Đỉnh \(A\) có toạ độ là các số dương, hai điểm \(B\) và \(C\) nằm trên trục \(Ox,\) phương trình cạnh \(AB\) là \(y = 3\sqrt 7 \left( {x - 1} \right).\) Biết chu vi tam giác \(ABC\) bằng \(18,\) tìm toạ độ các đỉnh \(A,\, B, \,C.\)
- A \(A\left( {2;3\sqrt 7 } \right);B\left( {1;0} \right);C\left( { - 3;0} \right)\)
- B \(A\left( {2;3\sqrt 7 } \right);B\left( {1;0} \right);C\left( {0; - 3} \right)\)
- C \(A\left( {2;3\sqrt 7 } \right);B\left( {1;0} \right);C\left( {3;0} \right)\)
- D \(A\left( {2;3\sqrt 7 } \right);B\left( {1;0} \right);C\left( { - 2;0} \right)\) \(\)
Phương pháp giải:
Sử dụng tính chất của tam giác cân và công thức tính chu vi tam giác để làm bài.
Lời giải chi tiết:
Theo đề bài ta có:
\(\begin{array}{l}\left\{ B \right\} = AB \cap Ox \Rightarrow B\left( {1;\,\,0} \right)\\A \in AB \Rightarrow A\left( {a;\,\,\,3\sqrt 7 \left( {a - 1} \right)} \right) \Rightarrow a > 1\,\,\,\,\left( {do{\rm{ }}{x_A} > 0,{y_A} > 0} \right)\end{array}\)
Gọi \(AH\) là đường cao của \(\Delta ABC \Rightarrow H\) là hình chiếu của \(A\) trên \(Ox\)
\( \Rightarrow H\left( {a;\,\,0} \right)\)
Mà \(\Delta ABC\) là \(\Delta \) cân tại \(A \Rightarrow H\) là trung điểm của \(BC\)
\(\begin{array}{l} \Rightarrow C\left( {2a - 1;0} \right) \Rightarrow \left\{ \begin{array}{l}\overrightarrow {BC} = \left( {2a - 2;\,\,0} \right)\\\overrightarrow {AB} = \left( {1 - a;\,\, - 3\sqrt 7 \left( {a - 1} \right)} \right)\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}BC = \sqrt {{{\left[ {2\left( {a - 1} \right)} \right]}^2}} = 2\left( {a - 1} \right)\,\,\,\,\left( {a > 1} \right)\\AC = AB = \sqrt {{{\left( {1 - a} \right)}^2} + 63\left( {a - 1} \right)} = 8\left( {a - 1} \right)\,\,\,\,\left( {a > 1} \right)\end{array} \right.\end{array}\)
Chu vi \(\Delta ABC\) là \(18 \Rightarrow AB + BC + CA = 18\)
\(\begin{array}{l}\, \Leftrightarrow \,2.8\left( {a - 1} \right) + 2\left( {a - 1} \right) = 18\\ \Leftrightarrow 18\left( {a - 1} \right) = 18\\ \Leftrightarrow a - 1 = 1\\ \Leftrightarrow a = 2\\ \Rightarrow \left\{ \begin{array}{l}C\left( {3;\,\,0} \right)\\A\left( {2;\,\,3\sqrt 7 } \right)\end{array} \right..\end{array}\)
Chọn C