Câu hỏi
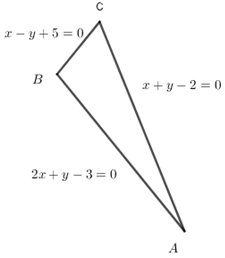
Cho tam giác ABC có phương trình \(\left( {AB} \right):\,\,2x + y - 3 = 0\), phương trình \(\left( {AC} \right):\,\,x + y - 2 = 0\) và phương trình \(\left( {BC} \right):x - y + 5 = 0\). Tìm tọa độ A ; B ; C.
- A \(A\left( {1;1} \right);B\left( {\frac{2}{3};\frac{{13}}{3}} \right);C\left( { - \frac{3}{2};\frac{7}{2}} \right)\)
- B \(A\left( {1;1} \right);B\left( { - \frac{2}{3};\frac{{13}}{3}} \right);C\left( { - \frac{3}{2};\frac{7}{2}} \right)\)
- C \(A\left( {1;1} \right);B\left( { - \frac{2}{3}; - \frac{{13}}{3}} \right);C\left( { - \frac{3}{2};\frac{7}{2}} \right)\)
- D \(A\left( {1;1} \right);B\left( { - \frac{2}{3}; - \frac{{13}}{3}} \right);C\left( {\frac{3}{2}; - \frac{7}{2}} \right)\)
Phương pháp giải:
Tọa độ điểm \(A\) là nghiệm của hệ phương trình gồm phương trình đường thẳng \(AC\) và \(AB.\) Giải hệ phương trình tìm tọa độ điểm \(A.\)
Tương tự với điểm \(B,\,\,C.\)
Lời giải chi tiết:
Toạ độ điểm A là nghiệm của hệ pt: \(\left\{ {\begin{array}{*{20}{c}}{2x + y - 3 = 0}\\{x + y - 2 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 1}\end{array}\,\, \Rightarrow A\left( {1;1} \right)} \right.} \right.\)
Toạ độ điểm B là nghiệm của hệ pt: \(\left\{ {\begin{array}{*{20}{c}}{2x + y - 3 = 0}\\{x - y + 5 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = - \frac{2}{3}}\\{y = \frac{{13}}{3}}\end{array}\,\, \Rightarrow B\left( { - \frac{2}{3};\frac{{13}}{3}} \right)} \right.} \right.\)
Toạ độ điểm C là nghiệm của hệ pt: \(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 = 0}\\{x - y + 5 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = - \frac{3}{2}}\\{y = \frac{7}{2}}\end{array}\,\, \Rightarrow C\left( { - \frac{3}{2};\frac{7}{2}} \right)} \right.} \right.\)
Chọn B.