Câu hỏi
Cho khối lăng trụ tam giác đều \(ABC.{A_1}{B_1}{C_1}\) có tất cả các cạnh bằng a. Gọi M là trung điểm của AA1. Thể tích khối chóp \(M.BC{A_1}\) là:
- A \(\dfrac{{{a^3}\sqrt 3 }}{{12}}\)
- B \(\dfrac{{{a^3}\sqrt 3 }}{{24}}\)
- C \(\dfrac{{{a^3}\sqrt 3 }}{6}\)
- D \(\dfrac{{{a^3}\sqrt 3 }}{8}\)
Lời giải chi tiết:
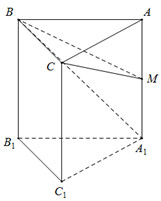
∆ ABC là tam giác đều cạnh a nên có diện tích
\({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Ta có \(AM = \dfrac{{A{A_1}}}{2} = \dfrac{a}{2}\)
Hai tứ diện MABC và MA1BC có chung đỉnh C, diện tích hai đáy MAB và MA1B bằng nhau nên có thể tích bằng nhau, suy ra
\({V_{M.BC{A_1}}} = {V_{M.ABC}} = \dfrac{1}{3}AM.{S_{ABC}} = \dfrac{{{a^3}\sqrt 3 }}{{24}}\)
Chọn B
Câu hỏi trước
