Câu hỏi
Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt đáy. Thể tích khối chóp là bao nhiêu biết \(SC = a\sqrt 3 \) ?
- A \(\dfrac{{2{a^3}\sqrt 6 }}{9}\)
- B \(\dfrac{{{a^3}\sqrt 6 }}{{12}}\)
- C \(\dfrac{{{a^3}\sqrt 3 }}{4}\)
- D \(\dfrac{{{a^3}\sqrt 3 }}{2}\)
Lời giải chi tiết:
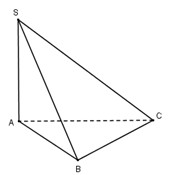
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}\left( {SAB} \right) \bot \left( {ABC} \right)\\\left( {SAC} \right) \bot \left( {ABC} \right)\\\left( {SAB} \right) \cap \left( {SAC} \right) = SA\end{array} \right\} \Rightarrow SA \bot \left( {ABC} \right)\\ \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}}\end{array}\)
\(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\) vuông tại A\( \Rightarrow SA = \sqrt {S{C^2} - A{C^2}} = \sqrt {3{a^2} - {a^2}} = a\sqrt 2 \)
Do tam giác ABC đều nên \({S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Vậy \({V_{S.ABC}} = \dfrac{1}{3}a\sqrt 2 .\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 6 }}{{12}}\)
Chọn B







