Lời giải chi tiết:

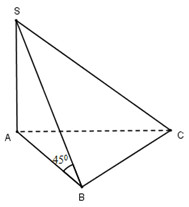
Vì SA vuông góc với mặt phẳng đáy nên AB là hình chiếu vuông góc của SB trên (ABC)

\( \Rightarrow \widehat {\left( {SB;\left( {ABC} \right)} \right)} = \widehat {\left( {SB,AB} \right)} = \widehat {SBA} = {45^o}\)

\( \Rightarrow \Delta SAB\)vuông cân tại A\( \Rightarrow SA = AB = a\)

Áp dụng công thức Hê rông, có

\({S_{ABC}} = \sqrt {p\left( {p - AB} \right)\left( {p - AC} \right)\left( {p - BC} \right)} \) \(\left( {p = \dfrac{{AB + BC + CA}}{2}} \right)\)

\(\begin{array}{l} = \dfrac{{{a^2}}}{4}\sqrt {\left( {1 + \sqrt 3  + \sqrt 5 } \right)\left( { - 1 + \sqrt 3  + \sqrt 5 } \right)\left( {1 - \sqrt 3  + \sqrt 5 } \right)\left( {1 + \sqrt 3  - \sqrt 5 } \right)} \\ = \dfrac{{{a^2}\sqrt {11} }}{4}\end{array}\)

Suy ra \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}a\dfrac{{{a^2}\sqrt {11} }}{4} = \dfrac{{\sqrt {11} }}{{12}}{a^3}\)

Chọn A