Câu hỏi
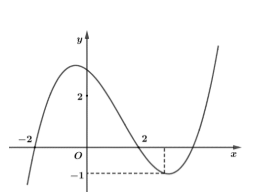
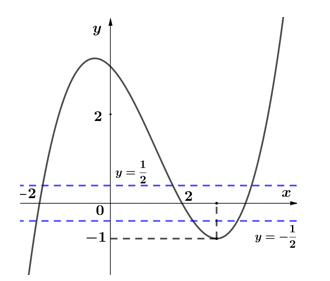
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình \(\left| {f\left( {{x^3} - 3x} \right)} \right| = \dfrac{1}{2}\) là:
- A 6.
- B 10.
- C 12.
- D 3.
Phương pháp giải:
Sử dụng số nghiệm của phương trình \(f\left( x \right) = m\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\)
Dựa vào đồ thị hàm số đã cho để tìm số nghiệm của phương trình.
Lời giải chi tiết:
Từ đồ thị hàm số ta có \(f\left( x \right) = \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x = a\,\,\left( { - 2 < a < 1} \right)\\x = b\,\,\left( {0 < b < 2} \right)\\x = c\,\,\left( {c > 2} \right)\end{array} \right.\) ; \(f\left( x \right) = - \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x = d\,\,\,\left( {d < - 2} \right)\\x = e\,\,\,\left( {e > 2} \right)\\x = f\,\,\left( {f > 2} \right)\end{array} \right.\)
Ta có \(\left| {f\left( {{x^3} - 3x} \right)} \right| = \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}f\left( {{x^3} - 3x} \right) = \dfrac{1}{2}\\f\left( {{x^3} - 3x} \right) = - \dfrac{1}{2}\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}{x^3} - 3x = a,\,\,\left( { - 2 < a < - 1} \right)\\{x^3} - 3x = b,\,\,\left( {0 < b < 2} \right)\\{x^3} - 3x = c,\,\,\left( {c > 2} \right)\\{x^3} - 3x = d,\,\,\left( {d < - 2} \right)\\{x^3} - 3x = e,\,\,\left( {e > 2} \right)\\{x^3} - 3x = f,\,\,\left( {f > 2} \right)\end{array} \right.\)
Xét hàm số \(y = {x^3} - 3x\); có \(y' = 3{x^2} - 3\)
Bảng biến thiên
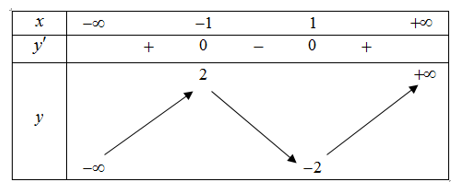
Dựa vào bảng biến thiên ta có
Phương trình: \({x^3} - 3x = a\) có 3 nghiệm.
Phương trình: \({x^3} - 3x = b\) có 3 nghiệm.
Phương trình: \({x^3} - 3x = c\) có 1 nghiệm.
Phương trình: \({x^3} - 3x = d\) có 1 nghiệm.
Phương trình: \({x^3} - 3x = e\) có 1 nghiệm.
Phương trình: \({x^3} - 3x = f\) có 1 nghiệm.
Vậy tổng có 10 nghiệm.
Chọn B.