Câu hỏi
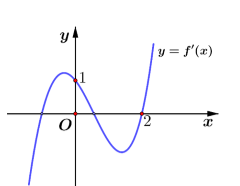
Cho hàm số \(f\left( x \right)\), hàm số \(y = f'\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Bất phương trình \(f\left( x \right) > x + m\) (\(m\) là tham số thực) nghiệm đúng với mọi \(x \in \left( {0\,;2} \right)\) khi và chỉ khi
- A \(m \le f\left( 2 \right) - 2\).
- B \(m < f\left( 2 \right) - 2\)
- C \(m \le f\left( 0 \right)\).
- D \(m < f\left( 0 \right)\).
Phương pháp giải:
Biến đổi đưa bất phương trình về dạng \(m < g\left( x \right)\) trên \(\left( {0;2} \right)\)
Lập BBT của hàm số \(y = g\left( x \right)\) trên \(\left( {0;2} \right)\) từ đó suy ra \(m\).
Lời giải chi tiết:
Ta có \(f\left( x \right) > x + m \Leftrightarrow m < f\left( x \right) - x\)
Bất phương trình \(f\left( x \right) > x + m\) nghiệm đúng với mọi \(x \in \left( {0\,;2} \right)\)
Hay \(m < f\left( x \right) - x\) nghiệm đúng với mọi \(x \in \left( {0\,;2} \right)\) (1)
Xét hàm số \(g\left( x \right) = f\left( x \right) - x\) trên khoảng \(\left( {0\,;2} \right)\)
Có \(g'\left( x \right) = f'\left( x \right) - 1\)
Từ đồ thị hàm \(y = f'\left( x \right)\) ta thấy \(f'\left( x \right) < 1\) với \(\forall x \in \left( {0;2} \right)\)
Nên \(g'\left( x \right) = f'\left( x \right) - 1 < 0\) với \(\forall x \in \left( {0;2} \right)\)
Bảng biến thiên hàm số \(y = g\left( x \right)\) trên \(\left( {0;2} \right)\)
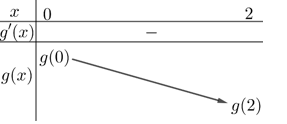
Vậy từ (1) suy ra \(m \le g\left( 2 \right)\)\( \Leftrightarrow m \le f\left( 2 \right) - 2\).
Chọn A.